Teoremi del triangolo isoscele¶
Il triangolo isoscele ha almeno due lati congruenti, l’eventuale lato non congruente si chiama base, i due lati congruenti si dicono lati obliqui.
Il triangolo equilatero è un caso particolare di triangolo isoscele: si dice che il triangolo equilatero è isoscele rispetto a qualsiasi lato preso come base.
Teorema diretto del triangoli isoscele¶
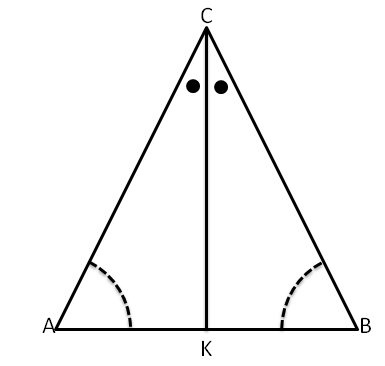
In un triangolo isoscele gli angoli alla base sono congruenti.
Ipotesi:
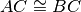
Tesi:
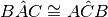
Dimostrazione
Tracciamo la bisettrice
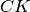 dell’angolo in
dell’angolo in
 .
.
I triangolo
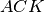 e
e
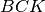 sono congruenti per il primo criterio, infatti hanno:
sono congruenti per il primo criterio, infatti hanno:
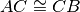 per ipotesi
per ipotesi
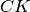 lato in comune
lato in comune
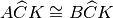 perché
perché
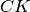 è la bisettrice dell’angoloin
è la bisettrice dell’angoloin
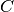 .
.
Pertanto, essendo congruenti hanno tutti gli elementi congruenti, in particolare
l’angolo in
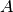 è congruente all’angolo in
è congruente all’angolo in
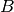 . Q.e.d.
. Q.e.d.
Il teorema precedente è invertibile, nel senso che è valido anche il teorema inverso, quello che si ottiene scambiando ipotesi e tesi.
Teorema inverso del triangoli isoscele¶
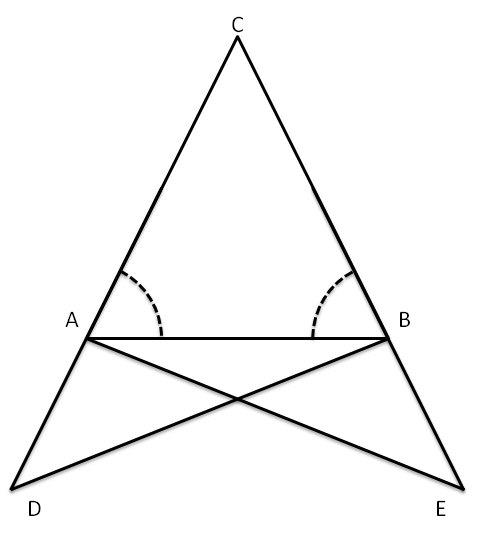
Se un triangolo ha due angoli congruenti, allora è isoscele (rispetto al lato compreso tra gli angoli congruenti preso come base).
Ipotesi:
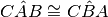
Tesi:
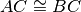
Dimostrazione: Procediamo per passi, realizzando una costruzione che ci permetta
di confrontare coppie di triangoli congruenti. Prolunghiamo i lati
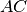 e
e
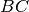 dalla parte di
dalla parte di
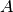 e di
e di
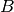 rispettivamente, e sui prolungamenti prendiamo due punti
rispettivamente, e sui prolungamenti prendiamo due punti
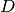 ed
ed
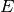 in maniera tale che risulti
in maniera tale che risulti
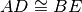 .
.
Osserviamo che i triangoli
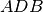 e
e
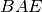 risultano congruenti per il 1° criterio, avendo in comune il lato
risultano congruenti per il 1° criterio, avendo in comune il lato
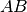 ed essendo
ed essendo
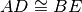 per costruzione e
per costruzione e
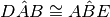 perché adiacenti agli angoli
perché adiacenti agli angoli
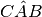 e
e
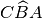 congruenti per ipotesi.Pertanto, tutti gli elementi dei due triangoli
congruenti per ipotesi.Pertanto, tutti gli elementi dei due triangoli
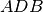 e
e
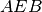 sono ordinatamente congruenti, in particolare
sono ordinatamente congruenti, in particolare
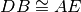 ,
,
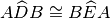
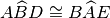 .
.
Confrontiamo ora i triangoli CDB e CAE ,risultano congruenti per il 2° criterio
poiché hanno
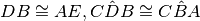 per quanto appena dimostrato e
per quanto appena dimostrato e
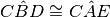 perché somma di angoli rispettivamente congruenti:
perché somma di angoli rispettivamente congruenti:
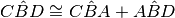 e
e
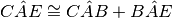 .
.
Pertanto, i restanti elementi dei due triangoli risultano ordinatamente congruenti:
In particolare
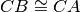 , che è la tesi che volevamo dimostrare. Q.e.d.
, che è la tesi che volevamo dimostrare. Q.e.d.
Dai due teoremi precedenti seguono importanti proprietà, che qui riportiamo come corollari.
Corollari¶
Un triangolo equilatero è anche equiangolo.
Viceversa, se un triangolo è equiangolo, allora è equilatero.
Un triangolo scaleno non ha angoli congruenti.
Viceversa, se un triangolo non ha angoli congruenti, allora è scaleno.
Dimostrazioni
- Poiché un triangolo equilatero è isoscele rispetto a qualsiasi lato preso come base, la tesi segue dal teorema diretto del triangolo isoscele.
- Possiamo confrontare gli angoli a due a due; risulteranno i lati congruenti a due a due in base al teorema inverso del triangolo isoscele.
- Se per assurdo un triangolo scaleno avesse due angoli congruenti, allora risulterebbe isoscele, in base al teorema inverso del triangolo isoscele.
- Se per assurdo un triangolo che non ha angoli congruenti non fosse scaleno, il che vuol dire che sarebbe isoscele, allora avrebbe angoli congruenti in contrasto con l’ipotesi di assurdo. Q.e.d.
Proprietà del triangolo isoscele¶
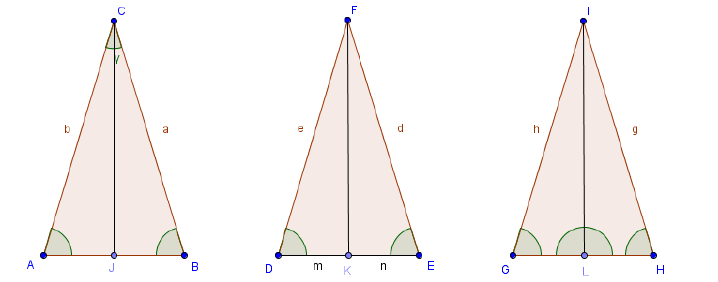
In ogni triangolo isoscele, la mediana relativa alla base è anche altezza e bisettrice.
In figura,
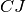 è per ipotesi la bisettrice dell’angolo al vertice del triangolo
è per ipotesi la bisettrice dell’angolo al vertice del triangolo
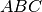 ,
,
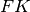 è la mediana relativa alla base
è la mediana relativa alla base
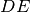 del triangolo
del triangolo
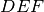 ,
,
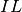 è l’altezza relativa alla base
è l’altezza relativa alla base
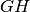 del triangolo
del triangolo
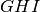 .
.
Dividiamo l’enunciato in tre parti:
a) In un triangolo isoscele la bisettrice dell’angolo al vertice è anche altezza e mediana relativa alla base.
b) In un triangolo isoscele la mediana relativa alla base è anche bisettrice dell’angolo al vertice e altezza relativa alla base.
c) In un triangolo isoscele l’altezza relativa alla base è anche bisettrice dell’angolo al vertice e mediana relativa alla base.
Dimostriamo le prime due parti della proposizione.
Per ciascuna delle tre parti precedenti, scriviamo ipotesi e tesi; utilizziamo i
tre triangoli della figura, segnaliamo che
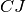 è per ipotesi la bisettrice dell’angolo al vertice del triangolo
è per ipotesi la bisettrice dell’angolo al vertice del triangolo
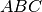 ,
,
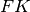 la mediana relativa alla base
la mediana relativa alla base
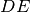 del triangolo
del triangolo
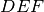 ,
,
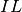 l’altezza relativa alla base
l’altezza relativa alla base
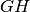 del triangolo
del triangolo
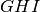 .
.
In
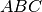 :
:
Ipotesi:
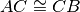 ,
,
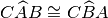 ,
,
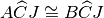
Tesi:
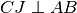 ,
,
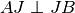 .
.
In
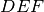 :
:
Ipotesi:,
,
.. tab
Tesi:
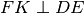 ,
,
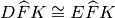 .
.
- In GHI:
Ipotesi:
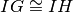 ,
,
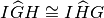 ,
,
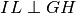
Tesi:
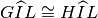 ,
,
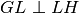 .
.
Avviamo la dimostrazione delle prime due parti, che lasciamo completare al lettore, rimandando al prossimo capitolo la dimostrazione della terza parte. Utilizziamo i primi due criteri di congruenza, i teoremi del triangolo isoscele e le nozioni comuni della geometria euclidea.
Dimostrazione a): I triangoli
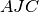 e
e
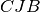 sono congruenti per il secondo criterio. Infatti… Dunque
sono congruenti per il secondo criterio. Infatti… Dunque
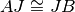 e
e
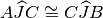 che risultano pertanto retti in quanto adiacenti.
che risultano pertanto retti in quanto adiacenti.
Dimostrazione b): I triangoli
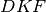 e
e
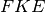 sono congruenti per il primo criterio. Infatti… Dunque
sono congruenti per il primo criterio. Infatti… Dunque
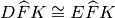 e
e
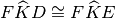 che risultano pertanto retti in quanto adiacenti. Q.e.d.
che risultano pertanto retti in quanto adiacenti. Q.e.d.
Esercizi¶
In un triangolo isoscele le mediane relative ai lati congruenti sono congruenti.
In un triangolo isoscele le bisettrici degli angoli alla base sono congruenti.
Due triangoli isosceli sono congruenti se hanno rispettivamente congruenti l’angolo al vertice e uno dei lati obliqui.
Due triangoli isosceli sono congruenti se hanno rispettivamente congruenti la base e uno degli angoli ad essa adiacenti.
Due triangoli isosceli sono congruenti se hanno rispettivamente congruenti la base e la bisettrice dell’angolo al vertice.
Due triangoli isosceli sono congruenti se hanno rispettivamente congruenti gli angoli al vertice e due lati corrispondenti qualsiasi.
Due triangoli, che hanno congruenti due lati e la mediana relativa ad uno dei due, sono congruenti.
In un triangolo isoscele
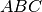 di base
di base
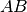 e vertice
e vertice
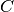 , prendi su
, prendi su
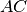 un punto
un punto
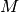 e su
e su
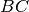 un punto
un punto
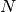 in modo che
in modo che
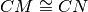 , quali delle seguenti coppie di triangoli sono congruenti? Dimostralo.
, quali delle seguenti coppie di triangoli sono congruenti? Dimostralo.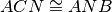
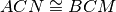
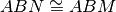
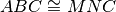
In un triangolo isoscele
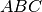 di base
di base
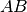 e vertice
e vertice
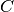 , indica con
, indica con
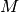 il punto medio di
il punto medio di
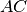 , con
, con
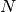 il punto medio di
il punto medio di
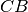 e con
e con
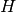 il punto medio di
il punto medio di
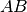 . Quali delle seguenti coppie di triangoli sono congruenti?
. Quali delle seguenti coppie di triangoli sono congruenti?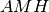 e
e
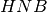
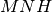 e
e

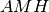 e
e
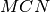
Sui lati
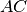 e
e
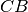 del triangolo isoscele
del triangolo isoscele
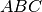 di base
di base
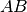 considera rispettivamente due punti
considera rispettivamente due punti
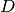 ed E tali che
ed E tali che
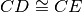 . Dimostra che i triangoli
. Dimostra che i triangoli
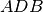 e
e
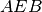 son congruenti. Detto
son congruenti. Detto
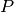 il punto di intersezione tra
il punto di intersezione tra
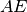 e
e
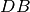 , dimostrare che
, dimostrare che
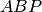 e
e
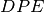 sono triangoli isosceli.
sono triangoli isosceli.In un triangolo isoscele
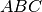 di base
di base
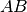 e vertice
e vertice
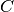 prolunga la base
prolunga la base
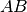 , dalla parte di
, dalla parte di
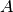 di un segmento
di un segmento
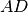 e dalla parte di
e dalla parte di
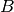 di un segmento
di un segmento
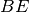 congruente ad
congruente ad
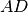 . Dimostra che anche il triangolo
. Dimostra che anche il triangolo
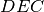 è isoscele.
è isoscele.Nel triangolo isoscele
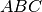 di base
di base
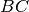 , prendi sul prolungamento di
, prendi sul prolungamento di
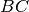 due segmenti congruenti
due segmenti congruenti
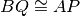 , dimostra che
, dimostra che
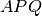 è isoscele.
è isoscele.Due triangoli isosceli
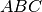 e
e
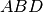 hanno in comune la base
hanno in comune la base
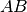 , i vertici
, i vertici
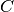 e
e
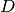 sono situati da parti opposte rispetto alla base
sono situati da parti opposte rispetto alla base
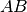 . Dimostra che la retta per
. Dimostra che la retta per
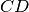 è bisettrice dell’angolo in
è bisettrice dell’angolo in
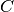 .
.In un triangolo isoscele
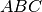 di base
di base
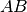 e vertice
e vertice
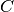 traccia le bisettrici
traccia le bisettrici
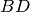 all’angolo in
all’angolo in
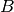 e
e
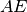 all’angolo in
all’angolo in
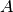 . Dimostra che
. Dimostra che
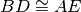 . Detto
. Detto
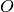 il punto di intersezione delle bisettrici dimostra che
il punto di intersezione delle bisettrici dimostra che
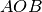 è isoscele. Dimostra che il triangolo
è isoscele. Dimostra che il triangolo
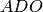 è congruente al triangolo
è congruente al triangolo
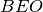 .
.In un triangolo isoscele
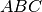 di base
di base
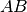 e vertice
e vertice
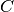 prolunga, dalla parte di
prolunga, dalla parte di
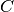 la bisettrice
la bisettrice
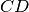 dell’angolo in
dell’angolo in
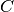 di un segmento
di un segmento
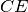 . Dimostra che
. Dimostra che
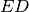 è bisettrice dell’angolo
è bisettrice dell’angolo
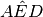 .
.In un triangolo isoscele
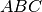 di base
di base
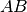 e vertice
e vertice
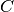 prendi su
prendi su
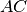 un punto
un punto
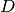 e su
e su
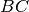 il punto E tali che
il punto E tali che
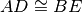 . Detto O il punto di intersezione di
. Detto O il punto di intersezione di
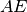 con
con
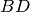 , dimostra che
, dimostra che
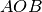 è isoscele.
è isoscele.In un triangolo
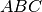 sia
sia
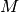 il punto medio di
il punto medio di
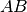 . Traccia la mediana
. Traccia la mediana
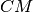 e prolungala dalla parte di
e prolungala dalla parte di
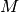 di un segmento
di un segmento
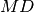 congruente a
congruente a
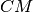 . Dopo aver dimostrato che il triangolo
. Dopo aver dimostrato che il triangolo
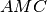 è congruente a
è congruente a
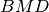 , dimostra che se
, dimostra che se
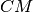 è bisettrice dell’angolo in
è bisettrice dell’angolo in
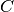 allora
allora
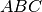 è isoscele.
è isoscele.In un triangolo isoscele
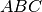 di base
di base
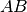 e vertice
e vertice
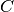 , prendi su
, prendi su
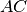 un punto
un punto
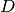 e su
e su
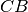 un punto E in modo che
un punto E in modo che
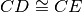 . Dimostra che il triangolo
. Dimostra che il triangolo
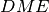 , dove
, dove
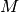 è il punto medio della base
è il punto medio della base
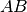 , è isoscele.
, è isoscele.Due triangoli isoscele hanno in comune la base,dimostra che la retta che unisce i vertici dei due triangoli divide la base a metà.
In un triangolo isoscele
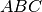 di base
di base
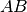 e vertice
e vertice
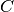 , si ha che
, si ha che
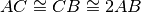 . Indica con
. Indica con
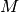 il punto medio di
il punto medio di
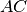 e
e
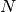 il punto medio di
il punto medio di
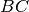 ,
,
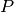 il punto di intersezione di
il punto di intersezione di
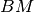 con
con
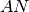 . Individua tutti i triangoli isosceli che si vengono a formare. Dimostra che
. Individua tutti i triangoli isosceli che si vengono a formare. Dimostra che
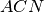 è congruente a
è congruente a
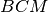 , che
, che
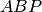 è isoscele, che
è isoscele, che
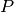 appartiene all’altezza
appartiene all’altezza
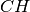 del triangolo.
del triangolo.Sia dato il triangolo
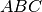 e sia
e sia
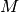 il punto medio del lato
il punto medio del lato
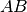 . Si prolunghi
. Si prolunghi
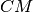 di un segmento
di un segmento
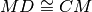 . Dimostrare che
. Dimostrare che
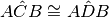 .
.Si prolunghino i lati
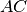 e
e
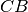 del triangolo isoscele ABC rispettivamente di due segmenti
del triangolo isoscele ABC rispettivamente di due segmenti
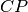 e
e
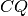 tra loro congruenti. Dimostrare che
tra loro congruenti. Dimostrare che
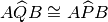 e che
e che
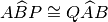 .
.Sulla base
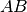 di un triangolo isoscele
di un triangolo isoscele
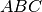 prendi i punti
prendi i punti
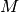 e
e
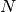 tali che
tali che
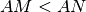 e
e
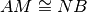 . Dimostra che
. Dimostra che
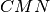 è isoscele.
è isoscele.Sia
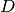 il punto di intersezione delle bisettrici degli angoli alla base di un
triangolo isoscele
il punto di intersezione delle bisettrici degli angoli alla base di un
triangolo isoscele
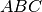 di vertice
di vertice
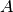 . Dimostra che
. Dimostra che
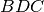 è isoscele.
è isoscele.Nel triangolo isoscele
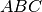 di base
di base
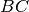 prolunga
prolunga
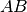 di un segmento
di un segmento
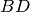 e
e
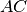 di un segmento
di un segmento
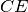 in modo che
in modo che
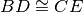 . Dimostra che
. Dimostra che
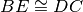 .
.